7014. Сражение за серебро

Пит Хейн был голландским военно-морским офицером во время Восьмидесятилетней войны между Соединенными Провинциями Нидерландов и Испании. Его самая известная победа заключалась в захвате в 1628 году около Кубы “Зильвервлота” (“Серебряный флот”), где он перехватил ряд испанских судов, перевозивших серебро из испанских колоний в Северной и Южной Америке в Испанию. Детали об этом знаменитом военно-морском сражении отрывочны, поэтому приведенное ниже описание может содержать некоторые исторические неточности.

Серебряный флот состоял из сосудов, содержащих серебряные монеты. Основная стратегия Пита Хейна была проста: отвести от флота несколько судов, чтобы захватить их содержимое.

Пытаясь помешать голландцам выполнить этот план, испанцы связали все корабли в своем флоте, используя огромные железные цепи. Каждое судно во флоте было прикреплено по меньшей мере к одному другому судну. Любые два судна соединялись не более чем одной цепью. И испанцы убедились, что цепи не пересекаются, иначе они могли бы завязаться в узел. Как результат, судна и цепи образовали связный плоский граф.

Тем не менее, испанские превентивные меры только ухудшили их положение. Как опытный военно-морской офицер, Пит Хейн знал, что отбуксировать группу кораблей легче всего, если каждые два корабля в ней будут соединены цепью. Он назвал такие группы цепными группами.

Пит Хейн приказал своим людям отбуксировать все корабли в группе, содержащей наибольшее количество добычи, после того как он разорвал их связи с оставшимися кораблями испанского флота несколькими высокоточными пушечными выстрелами. Общая добыча в цепной группе – это общее количество серебряных монет в суднах, ее составляющих.

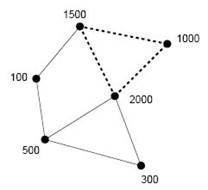
Серебряный флот представлен в виде графа: каждая точка обозначает судно во флоте, а каждая линия обозначает цепь, соединяющую два судна. Судна, которые соединены на рисунке пунктирными линиями, соответствуют группе, которая обеспечивает наибольшее суммарное значение серебряных монет. В этом случае, Пит Хейн добывает 4500 серебряных монет из флота.

Имея описание Серебряного флота, найдите ценность группы с наибольшим количеством добычи (то есть общее количество серебряных монет на кораблях, входящих в состав группы).

Вход. Для каждого теста:

· Строка содержит два целых числа v (2 ≤ v ≤ 450) и e (1 ≤ e ≤ 900) – число суден во флоте и число цепей.

· Следующие v строк задают s₁, s₂, ..., s_v – количество серебряных монет, которое везет судно номер i (1 ≤ i ≤ v). Числа s_i являются натуральными, причем 100 ≤ s_i ≤ 6000.

· Далее для каждой цепи задана строка из двух целых чисел cstart и cend – номера суден, соединенных цепью (1 ≤ cstart < cend ≤ v).

Каждый флот образует связный плоский граф.

Выход. Для каждого теста вывести в отдельной строке количество серебряных монет, захваченных флотом Пита Хейна.

Пример входа	Пример выхода
4 6 100 5000 1000 2000 1 2 1 3 1 4 2 3 2 4 3 4 6 8 1500 1000 100 2000 500 300 1 2 1 3 1 4 2 4 3 5 4 5 4 6 5 6	8100 4500

РЕШЕНИЕ

клика в планарном графе

Анализ алгоритма

Рассмотрим граф, вершинами которого являются корабли Серебряного флота. По условию он планарный. В нем следует найти клику, корабли которых везут максимальное количество серебряных монет.

По теореме Куратовского планарный граф может иметь максимум клику размера 4. Перебираем в графе все клики размером 2, 3, 4 и среди них ищем ту, которая содержит наибольшее количество серебряных монет.

Рассмотрим пример, когда клика из двух вершин {1, 5} содержит больше монет, чем клика из четырех вершин {1, 2, 3, 4}.

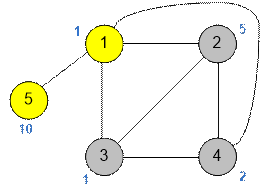
Пример

Графы, приведенные в примере, имеют вид:

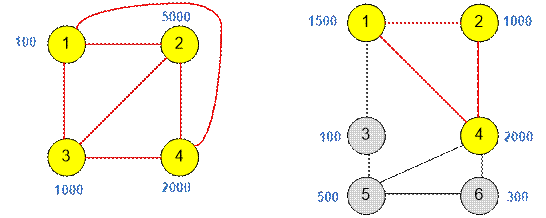
Первый граф содержит клику из четырех вершин, суммарное количество монет в ней равно 8100.

Во втором графе наибольшее количество монет содержится в клике из трех вершин 1, 2 и 4, суммарное количество монет в ней равно 4500.

Реализация алгоритма

Матрицу смежности графа храним в двумерном массиве m. Количество серебряных монет, которое везет i-ое судно, храним в p[i].

int m[460][460];

int p[460];

Основная часть программы. Обрабатываем несколько тестов. Читаем количество вершин v и ребер e графа.

while (scanf("%d %d", &v, &e) == 2)

{

memset(m, 0, sizeof(m));

res = -1;

Читаем количество серебряных монет, которое везут судна.

for (i = 1; i <= v; i++)

{

scanf("%d", &p[i]);

if (p[i] > res) res = p[i]; // clique of size 1

}

Читаем список ребер графа. Строим матрицу смежности.

for (i = 1; i <= e; i++)

{

scanf("%d %d", &a, &b);

m[a][b] = m[b][a] = 1;

}

Перебираем пары вершин.

for (i = 1; i < v; i++)

for (j = i + 1; j <= v; j++)

Если между вершинами i и j есть ребро, то рассматриваем клику размера 2.

if (m[i][j])

{

Наибольшее количество монет в кликах размера 2 заносим в res.

if (p[i] + p[j] > res)

res = p[i] + p[j]; // clique of size 2

Перебираем третью вершину k.

for (k = j + 1; k <= v; k++)

Если вершины i, j и k образуют клику, то заносим в res наибольшее количество монет в кликах размера 3.

if (m[i][k] && m[j][k])

{

if (p[i] + p[j] + p[k] > res)

res = p[i] + p[j] + p[k]; // clique of size 3

Перебираем четвертую вершину l.

for (l = k + 1; l <= v; l++)

Если вершины i, j, k и l образуют клику, то заносим в res наибольшее количество монет в кликах размера 4.

if (m[i][l] && m[j][l] && m[k][l])

{

if (p[i] + p[j] + p[k] + p[l] > res)

res = p[i] + p[j] + p[k] + p[l]; // clique of size 4

}

}

}

Выводим ответ.

printf("%d\n", res);

}